% S. Boyd, et. al., "Convex Optimization of Graph Laplacian Eigenvalues"
% ICM'06 talk examples (www.stanford.edu/~boyd/cvx_opt_graph_lapl_eigs.html)
% Written for CVX by Almir Mutapcic 08/29/06
% (figures are generated)
%
% In this example we consider a graph described by the incidence matrix A.
% Each edge has a weight W_i, and we optimize various functions of the
% edge weights as described in the referenced paper; in particular,
%
% - the fastest distributed linear averaging (FDLA) problem (fdla.m)
% - the fastest mixing Markov chain (FMMC) problem (fmmc.m)
%
% Then we compare these solutions to the heuristics listed below:
%
% - maximum-degree heuristic (max_deg.m)
% - constant weights that yield fastest averaging (best_const.m)
% - Metropolis-Hastings heuristic (mh.m)

% randomly generate a graph with 50 nodes and 200 edges
% and make it pretty for plotting
n = 50; threshold = 0.2529;
rand('state',209);
xy = rand(n,2);

angle = 10*pi/180;
Rotate = [ cos(angle) sin(angle); -sin(angle) cos(angle) ];
xy = (Rotate*xy')';

Dist = zeros(n,n);
for i=1:(n-1);
  for j=i+1:n;
    Dist(i,j) = norm( xy(i,:) - xy(j,:) );
  end;
end;
Dist = Dist + Dist';
Ad = Dist < threshold;
Ad = Ad - eye(n);
m = sum(sum(Ad))/2;

% find the incidence matrix
A = zeros(n,m);
l = 0;
for i=1:(n-1);
  for j=i+1:n;
    if Ad(i,j)>0.5
      l = l + 1;
      A(i,l) =  1;
      A(j,l) = -1;
    end;
  end;
end;
A = sparse(A);

% Compute edge weights: some optimal, some based on heuristics
[n,m] = size(A);

[ w_fdla, rho_fdla ] = fdla(A);
[ w_fmmc, rho_fmmc ] = fmmc(A);
[ w_md,   rho_md   ] = max_deg(A);
[ w_bc,   rho_bc   ] = best_const(A);
[ w_mh,   rho_mh   ] = mh(A);

tau_fdla = 1/log(1/rho_fdla);
tau_fmmc = 1/log(1/rho_fmmc);
tau_md   = 1/log(1/rho_md);
tau_bc   = 1/log(1/rho_bc);
tau_mh   = 1/log(1/rho_mh);

eig_opt  = sort(eig(eye(n) - A * diag(w_fdla) * A'));
eig_fmmc = sort(eig(eye(n) - A * diag(w_fmmc) * A'));
eig_mh   = sort(eig(eye(n) - A * diag(w_mh)   * A'));
eig_md   = sort(eig(eye(n) - A * diag(w_md)   * A'));
eig_bc   = sort(eig(eye(n) - A * diag(w_bc)   * A'));

fprintf(1,'\nResults:\n');
fprintf(1,'FDLA weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_fdla,tau_fdla);
fprintf(1,'FMMC weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_fmmc,tau_fmmc);
fprintf(1,'M-H weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_mh,tau_mh);
fprintf(1,'MAX_DEG weights:\t rho = %5.4f \t tau = %5.4f\n',rho_md,tau_md);
fprintf(1,'BEST_CONST weights:\t rho = %5.4f \t tau = %5.4f\n',rho_bc,tau_bc);

% plot results
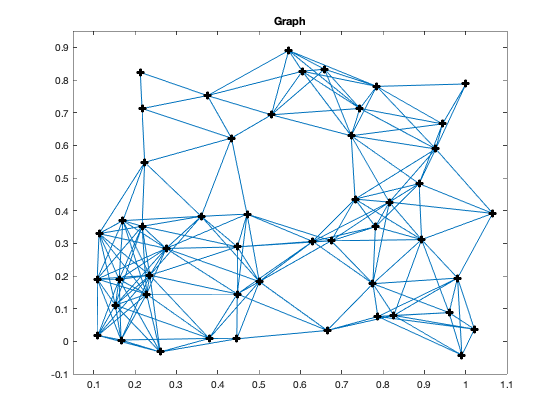
figure(1), clf
gplot(Ad,xy);
hold on;
plot(xy(:,1), xy(:,2), 'ko','LineWidth',4, 'MarkerSize',4);
axis([0.05 1.1 -0.1 0.95]);
title('Graph')
hold off;

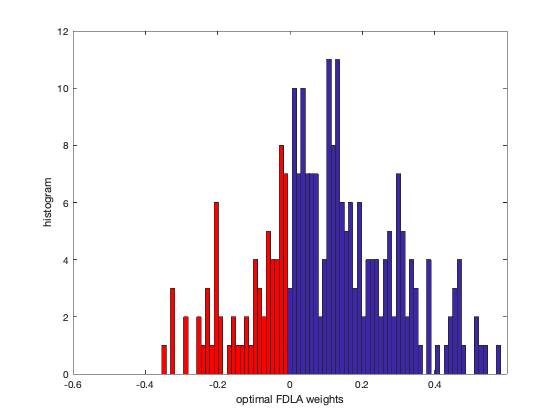
figure(2), clf
v_fdla = [w_fdla; diag(eye(n) - A*diag(w_fdla)*A')];
[ifdla, jfdla, neg_fdla] = find( v_fdla.*(v_fdla < -0.001 ) );
v_fdla(ifdla) = [];
wbins = [-0.6:0.012:0.6];
hist(neg_fdla,wbins); hold on,
h = findobj(gca,'Type','patch');
set(h,'FaceColor','r')
hist(v_fdla,wbins); hold off,
axis([-0.6 0.6 0 12]);
xlabel('optimal FDLA weights');
ylabel('histogram');

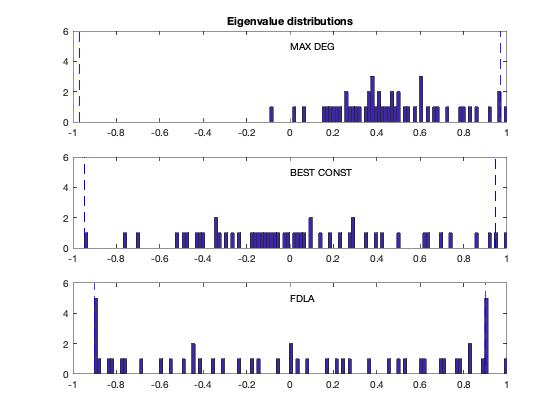
figure(3), clf
xbins = (-1:0.015:1)';
ymax  = 6;
subplot(3,1,1)
hist(eig_md, xbins); hold on;
max_md = max(abs(eig_md(1:n-1)));
plot([-max_md -max_md],[0 ymax], 'b--');
plot([ max_md  max_md],[0 ymax], 'b--');
axis([-1 1 0 ymax]);
text(0,5,'MAX DEG');
title('Eigenvalue distributions')
subplot(3,1,2)
hist(eig_bc, xbins); hold on;
max_opt = max(abs(eig_bc(1:n-1)));
plot([-max_opt -max_opt],[0 ymax], 'b--');
plot([ max_opt  max_opt],[0 ymax], 'b--');
axis([-1 1 0 ymax]);
text(0,5,'BEST CONST');
subplot(3,1,3)
hist(eig_opt, xbins); hold on;
max_opt = max(abs(eig_opt(1:n-1)));
plot([-max_opt -max_opt],[0 ymax], 'b--');
plot([ max_opt  max_opt],[0 ymax], 'b--');
axis([-1 1 0 ymax]);
text(0,5,'FDLA');

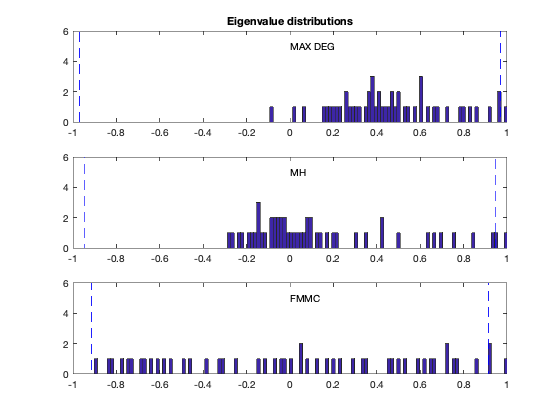
figure(4), clf
xbins = (-1:0.015:1)';
ymax  = 6;
subplot(3,1,1)
hist(eig_md, xbins); hold on;
max_md = max(abs(eig_md(1:n-1)));
plot([-max_md -max_md],[0 ymax], 'b--');
plot([ max_md  max_md],[0 ymax], 'b--');
axis([-1 1 0 ymax]);
text(0,5,'MAX DEG');
title('Eigenvalue distributions')
subplot(3,1,2)
hist(eig_mh, xbins); hold on;
max_opt = max(abs(eig_mh(1:n-1)));
plot([-max_opt -max_opt],[0 ymax], 'b--');
plot([ max_opt  max_opt],[0 ymax], 'b--');
axis([-1 1 0 ymax]);
text(0,5,'MH');
subplot(3,1,3)
hist(eig_fmmc, xbins); hold on;
max_opt = max(abs(eig_fmmc(1:n-1)));
plot([-max_opt -max_opt],[0 ymax], 'b--');
plot([ max_opt  max_opt],[0 ymax], 'b--');
axis([-1 1 0 ymax]);
text(0,5,'FMMC');

figure(5), clf
v_fmmc = [w_fmmc; diag(eye(n) - A*diag(w_fmmc)*A')];
[ifmmc, jfmmc, nonzero_fmmc] = find( v_fmmc.*(v_fmmc > 0.001 ) );
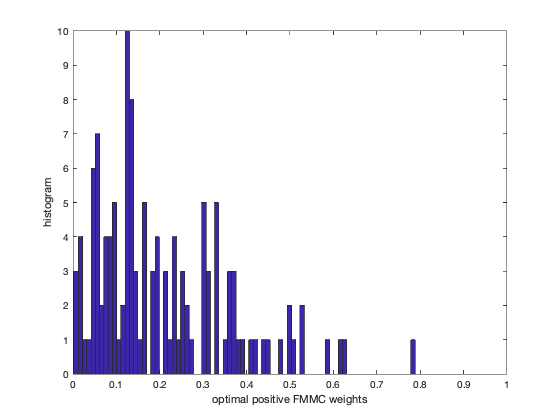
hist(nonzero_fmmc,80);
axis([0 1 0 10]);
xlabel('optimal positive FMMC weights');
ylabel('histogram');

figure(6), clf
An = abs(A*diag(w_fmmc)*A');
An = (An - diag(diag(An))) > 0.0001;
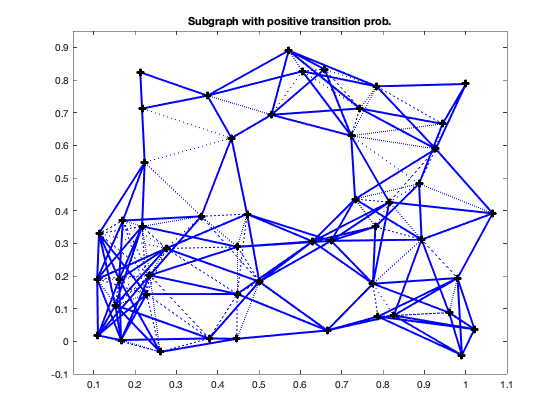
gplot(An,xy,'b-'); hold on;
h = findobj(gca,'Type','line');
set(h,'LineWidth',2.5)
gplot(Ad,xy,'b:');
plot(xy(:,1), xy(:,2), 'ko','LineWidth',4, 'MarkerSize',4);
axis([0.05 1.1 -0.1 0.95]);
title('Subgraph with positive transition prob.')
hold off;

 
Calling Mosek 9.1.9: 2598 variables, 249 equality constraints
   For improved efficiency, Mosek is solving the dual problem.
------------------------------------------------------------

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86

Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 249             
  Cones                  : 0               
  Scalar variables       : 48              
  Matrix variables       : 2               
  Integer variables      : 0               

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries                  : 1                 time                   : 0.00            
Lin. dep.  - tries                  : 1                 time                   : 0.00            
Lin. dep.  - number                 : 0               
Presolve terminated. Time: 0.00    
Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 249             
  Cones                  : 0               
  Scalar variables       : 48              
  Matrix variables       : 2               
  Integer variables      : 0               

Optimizer  - threads                : 8               
Optimizer  - solved problem         : the primal      
Optimizer  - Constraints            : 249
Optimizer  - Cones                  : 1
Optimizer  - Scalar variables       : 49                conic                  : 49              
Optimizer  - Semi-definite variables: 2                 scalarized             : 2550            
Factor     - setup time             : 0.00              dense det. time        : 0.00            
Factor     - ML order time          : 0.00              GP order time          : 0.00            
Factor     - nonzeros before factor : 3.14e+04          after factor           : 3.14e+04        
Factor     - dense dim.             : 2                 flops                  : 6.45e+06        
ITE PFEAS    DFEAS    GFEAS    PRSTATUS   POBJ              DOBJ              MU       TIME  
0   2.5e+01  1.9e+00  1.0e+00  0.00e+00   0.000000000e+00   0.000000000e+00   1.0e+00  0.01  
1   3.6e+00  2.9e-01  1.8e-01  -6.04e-01  -3.145391692e+00  -2.056927657e+00  1.5e-01  0.02  
2   1.3e+00  1.0e-01  1.0e-02  1.99e+00   -1.249328523e+00  -1.278489247e+00  5.1e-02  0.03  
3   4.6e-01  3.6e-02  2.5e-03  2.21e+00   -9.244695165e-01  -9.239620619e-01  1.9e-02  0.03  
4   1.3e-01  1.0e-02  4.0e-04  1.06e+00   -9.370436579e-01  -9.366043839e-01  5.4e-03  0.04  
5   3.2e-02  2.5e-03  4.5e-05  1.07e+00   -9.092458032e-01  -9.091799559e-01  1.3e-03  0.04  
6   9.7e-03  7.6e-04  7.5e-06  1.02e+00   -9.036651155e-01  -9.036585013e-01  3.9e-04  0.05  
7   2.6e-03  2.1e-04  1.0e-06  1.00e+00   -9.025198915e-01  -9.025209039e-01  1.1e-04  0.05  
8   7.7e-04  6.0e-05  1.6e-07  1.00e+00   -9.022541908e-01  -9.022552430e-01  3.1e-05  0.05  
9   1.9e-04  1.5e-05  1.9e-08  1.00e+00   -9.021233047e-01  -9.021236033e-01  7.5e-06  0.06  
10  5.0e-05  3.9e-06  2.7e-09  1.00e+00   -9.020926809e-01  -9.020927928e-01  2.0e-06  0.06  
11  9.3e-06  7.3e-07  2.1e-10  1.00e+00   -9.020810279e-01  -9.020810492e-01  3.7e-07  0.07  
12  1.6e-06  1.3e-07  1.5e-11  1.00e+00   -9.020790866e-01  -9.020790906e-01  6.5e-08  0.07  
13  3.8e-07  3.0e-08  1.7e-12  9.99e-01   -9.020787662e-01  -9.020787672e-01  1.5e-08  0.08  
14  1.5e-07  1.1e-08  4.1e-13  9.84e-01   -9.020786985e-01  -9.020786989e-01  5.7e-09  0.08  
15  3.5e-08  1.5e-09  1.9e-14  9.93e-01   -9.020786666e-01  -9.020786666e-01  7.3e-10  0.09  
Optimizer terminated. Time: 0.09    


Interior-point solution summary
  Problem status  : PRIMAL_AND_DUAL_FEASIBLE
  Solution status : OPTIMAL
  Primal.  obj: -9.0207866659e-01   nrm: 1e+00    Viol.  con: 5e-08    var: 0e+00    barvar: 0e+00  
  Dual.    obj: -9.0207866663e-01   nrm: 1e+00    Viol.  con: 0e+00    var: 6e-10    barvar: 1e-09  
Optimizer summary
  Optimizer                 -                        time: 0.09    
    Interior-point          - iterations : 15        time: 0.09    
      Basis identification  -                        time: 0.00    
        Primal              - iterations : 0         time: 0.00    
        Dual                - iterations : 0         time: 0.00    
        Clean primal        - iterations : 0         time: 0.00    
        Clean dual          - iterations : 0         time: 0.00    
    Simplex                 -                        time: 0.00    
      Primal simplex        - iterations : 0         time: 0.00    
      Dual simplex          - iterations : 0         time: 0.00    
    Mixed integer           - relaxations: 0         time: 0.00    

------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.902079
 
 
Calling Mosek 9.1.9: 2849 variables, 250 equality constraints
   For improved efficiency, Mosek is solving the dual problem.
------------------------------------------------------------

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86

Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 250             
  Cones                  : 0               
  Scalar variables       : 299             
  Matrix variables       : 2               
  Integer variables      : 0               

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries                  : 1                 time                   : 0.00            
Lin. dep.  - tries                  : 1                 time                   : 0.00            
Lin. dep.  - number                 : 0               
Presolve terminated. Time: 0.00    
Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 250             
  Cones                  : 0               
  Scalar variables       : 299             
  Matrix variables       : 2               
  Integer variables      : 0               

Optimizer  - threads                : 8               
Optimizer  - solved problem         : the primal      
Optimizer  - Constraints            : 250
Optimizer  - Cones                  : 1
Optimizer  - Scalar variables       : 300               conic                  : 50              
Optimizer  - Semi-definite variables: 2                 scalarized             : 2550            
Factor     - setup time             : 0.00              dense det. time        : 0.00            
Factor     - ML order time          : 0.00              GP order time          : 0.00            
Factor     - nonzeros before factor : 3.16e+04          after factor           : 3.16e+04        
Factor     - dense dim.             : 2                 flops                  : 6.58e+06        
ITE PFEAS    DFEAS    GFEAS    PRSTATUS   POBJ              DOBJ              MU       TIME  
0   9.9e+01  1.9e+00  1.0e+00  0.00e+00   0.000000000e+00   0.000000000e+00   1.0e+00  0.01  
1   6.4e+01  1.3e+00  3.8e-01  2.96e+00   -2.785394606e-01  -2.804109346e-01  6.5e-01  0.02  
2   3.8e+01  7.4e-01  1.7e-01  8.75e-01   -5.839164777e-01  -6.001269343e-01  3.8e-01  0.02  
3   9.9e+00  1.9e-01  1.4e-02  1.27e+00   -8.650800893e-01  -8.900123962e-01  1.0e-01  0.03  
4   1.7e+00  3.3e-02  9.0e-04  1.41e+00   -9.423735341e-01  -9.459175018e-01  1.7e-02  0.03  
5   4.1e-01  8.0e-03  1.0e-04  1.09e+00   -9.346101522e-01  -9.354588037e-01  4.1e-03  0.04  
6   2.3e-01  4.5e-03  4.2e-05  1.05e+00   -9.257160899e-01  -9.261948958e-01  2.3e-03  0.04  
7   1.4e-01  2.7e-03  2.0e-05  1.03e+00   -9.228175104e-01  -9.231092574e-01  1.4e-03  0.05  
8   7.5e-02  1.5e-03  7.7e-06  1.03e+00   -9.196176415e-01  -9.197761238e-01  7.5e-04  0.05  
9   5.3e-02  1.0e-03  4.6e-06  1.02e+00   -9.189122019e-01  -9.190252141e-01  5.4e-04  0.05  
10  1.9e-02  3.8e-04  9.7e-07  1.02e+00   -9.166447925e-01  -9.166864379e-01  1.9e-04  0.06  
11  1.0e-02  2.1e-04  3.9e-07  1.01e+00   -9.161236842e-01  -9.161465817e-01  1.1e-04  0.06  
12  3.4e-03  6.6e-05  7.0e-08  1.01e+00   -9.154785029e-01  -9.154858830e-01  3.4e-05  0.07  
13  1.5e-03  3.0e-05  2.2e-08  1.00e+00   -9.153103150e-01  -9.153137404e-01  1.6e-05  0.07  
14  8.1e-04  1.6e-05  8.1e-09  1.00e+00   -9.152413689e-01  -9.152431602e-01  8.1e-06  0.08  
15  1.7e-04  3.4e-06  8.0e-10  1.00e+00   -9.151721697e-01  -9.151725596e-01  1.8e-06  0.08  
16  4.2e-05  8.3e-07  9.5e-11  1.00e+00   -9.151569060e-01  -9.151570010e-01  4.3e-07  0.09  
17  5.1e-06  9.9e-08  4.0e-12  1.00e+00   -9.151521696e-01  -9.151521811e-01  5.1e-08  0.09  
18  2.7e-07  5.3e-09  4.9e-14  1.00e+00   -9.151515708e-01  -9.151515714e-01  2.7e-09  0.10  
19  2.0e-08  2.4e-08  9.8e-16  1.00e+00   -9.151515390e-01  -9.151515391e-01  2.0e-10  0.11  
Optimizer terminated. Time: 0.11    


Interior-point solution summary
  Problem status  : PRIMAL_AND_DUAL_FEASIBLE
  Solution status : OPTIMAL
  Primal.  obj: -9.1515153901e-01   nrm: 1e+00    Viol.  con: 7e-09    var: 4e-11    barvar: 0e+00  
  Dual.    obj: -9.1515153906e-01   nrm: 2e+00    Viol.  con: 0e+00    var: 7e-11    barvar: 8e-09  
Optimizer summary
  Optimizer                 -                        time: 0.11    
    Interior-point          - iterations : 19        time: 0.11    
      Basis identification  -                        time: 0.00    
        Primal              - iterations : 0         time: 0.00    
        Dual                - iterations : 0         time: 0.00    
        Clean primal        - iterations : 0         time: 0.00    
        Clean dual          - iterations : 0         time: 0.00    
    Simplex                 -                        time: 0.00    
      Primal simplex        - iterations : 0         time: 0.00    
      Dual simplex          - iterations : 0         time: 0.00    
    Mixed integer           - relaxations: 0         time: 0.00    

------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.915152
 

Results:
FDLA weights:		 rho = 0.9021 	 tau = 9.7037
FMMC weights:		 rho = 0.9152 	 tau = 11.2783
M-H weights:		 rho = 0.9489 	 tau = 19.0839
MAX_DEG weights:	 rho = 0.9706 	 tau = 33.5236
BEST_CONST weights:	 rho = 0.9470 	 tau = 18.3549