randn('seed',0);
n = 2;
m = 2*n;
A1 = [1 1; 1 -1; -1 1; -1 -1];
A2 = [1 0; -1 0; 0 1; 0 -1];
b1 = 2*ones(m,1);
b2 = [5; -3; 4; -2];
fprintf(1,'Finding a separating hyperplane between the 2 polyhedra...');
cvx_begin
variables lam(m) muu(m) z(n)
maximize ( -b1'*lam - b2'*muu)
A1'*lam + z == 0;
A2'*muu - z == 0;
norm(z) <= 1;
-lam <=0;
-muu <=0;
cvx_end
fprintf(1,'Done! \n');
disp('------------------------------------------------------------------');
disp('The distance between the 2 polyhedra C and D is: ' );
disp(['dist(C,D) = ' num2str(cvx_optval)]);
t = linspace(-3,6,100);
p = -z(1)*t/z(2) + (muu'*b2 - lam'*b1)/(2*z(2));
figure;
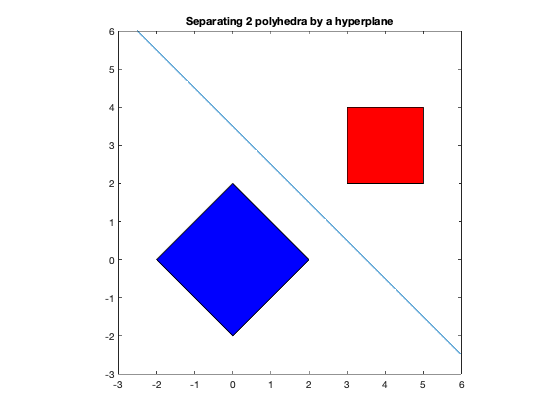
fill([-2; 0; 2; 0],[0;2;0;-2],'b', [3;5;5;3],[2;2;4;4],'r')
axis([-3 6 -3 6])
axis square
hold on;
plot(t,p)
title('Separating 2 polyhedra by a hyperplane');
Finding a separating hyperplane between the 2 polyhedra...
Calling Mosek 9.1.9: 12 variables, 5 equality constraints
------------------------------------------------------------
MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 5
Cones : 1
Scalar variables : 12
Matrix variables : 0
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.00
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 5
Cones : 1
Scalar variables : 12
Matrix variables : 0
Integer variables : 0
Optimizer - threads : 8
Optimizer - solved problem : the primal
Optimizer - Constraints : 4
Optimizer - Cones : 1
Optimizer - Scalar variables : 11 conic : 3
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 10 after factor : 10
Factor - dense dim. : 0 flops : 8.60e+01
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 1.0e+00 5.0e+00 2.0e+00 0.00e+00 0.000000000e+00 -1.000000000e+00 1.0e+00 0.00
1 3.9e-01 2.0e+00 7.7e-01 -2.28e-01 -1.913219675e+00 -2.202778981e+00 3.9e-01 0.01
2 7.5e-02 3.8e-01 6.3e-02 6.30e-01 -2.617880098e+00 -2.707045863e+00 7.5e-02 0.01
3 1.0e-02 5.0e-02 3.1e-03 9.27e-01 -2.148987477e+00 -2.160441677e+00 1.0e-02 0.01
4 4.0e-04 2.0e-03 2.6e-05 9.88e-01 -2.122427666e+00 -2.122892104e+00 4.0e-04 0.01
5 8.7e-06 4.4e-05 8.2e-08 1.00e+00 -2.121345336e+00 -2.121355382e+00 8.7e-06 0.01
6 1.9e-07 9.6e-07 2.7e-10 1.00e+00 -2.121320938e+00 -2.121321158e+00 1.9e-07 0.01
7 4.0e-09 2.0e-08 8.0e-13 1.00e+00 -2.121320357e+00 -2.121320361e+00 4.0e-09 0.01
Optimizer terminated. Time: 0.01
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: -2.1213203566e+00 nrm: 1e+00 Viol. con: 1e-12 var: 4e-09 cones: 0e+00
Dual. obj: -2.1213203612e+00 nrm: 4e+00 Viol. con: 0e+00 var: 4e-08 cones: 0e+00
Optimizer summary
Optimizer - time: 0.01
Interior-point - iterations : 7 time: 0.01
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +2.12132
Done!
------------------------------------------------------------------
The distance between the 2 polyhedra C and D is:
dist(C,D) = 2.1213