seed = 0;
randn('state',seed);
rand('state',seed);
delta = 1e-8;
m = 100;
n = 50;
A = randn(m,n);
x0 = randn(n,1);
b = A*x0 + rand(m,1);
fprintf(1, 'Finding a sparse feasible point using l1-norm heuristic ...')
cvx_begin
variable x_l1(n)
minimize( norm( x_l1, 1 ) )
subject to
A*x_l1 <= b;
cvx_end
nnz = length(find( abs(x_l1) > delta ));
fprintf(1,['\nFound a feasible x in R^%d that has %d nonzeros ' ...
'using the l1-norm heuristic.\n'],n,nnz);
NUM_RUNS = 15;
nnzs = [];
W = ones(n,1);
disp([char(10) 'Log-based heuristic:']);
for k = 1:NUM_RUNS
cvx_begin quiet
variable x_log(n)
minimize( sum( W.*abs(x_log) ) )
subject to
A*x_log <= b;
cvx_end
nnz = length(find( abs(x_log) > delta ));
nnzs = [nnzs nnz];
fprintf(1,' found a solution with %d nonzeros...\n', nnz);
W = 1./(delta + abs(x_log));
end
nnz = length(find( abs(x_log) > delta ));
fprintf(1,['\nFound a feasible x in R^%d that has %d nonzeros ' ...
'using the log heuristic.\n'],n,nnz);
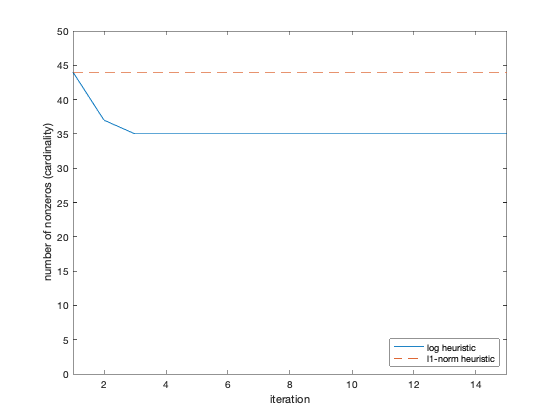
plot(1:NUM_RUNS, nnzs, [1 NUM_RUNS],[nnzs(1) nnzs(1)],'--');
axis([1 NUM_RUNS 0 n])
xlabel('iteration'), ylabel('number of nonzeros (cardinality)');
legend('log heuristic','l1-norm heuristic','Location','SouthEast')
Finding a sparse feasible point using l1-norm heuristic ...
Calling Mosek 9.1.9: 200 variables, 100 equality constraints
------------------------------------------------------------
MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 100
Cones : 50
Scalar variables : 200
Matrix variables : 0
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.00
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 100
Cones : 50
Scalar variables : 200
Matrix variables : 0
Integer variables : 0
Optimizer - threads : 8
Optimizer - solved problem : the primal
Optimizer - Constraints : 100
Optimizer - Cones : 50
Optimizer - Scalar variables : 200 conic : 100
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 5050 after factor : 5050
Factor - dense dim. : 0 flops : 1.35e+06
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 6.9e+00 0.0e+00 5.1e+01 0.00e+00 5.000000000e+01 0.000000000e+00 1.0e+00 0.00
1 2.5e+00 1.2e-15 1.1e+01 1.52e-01 4.011789130e+01 1.918514069e+01 3.5e-01 0.01
2 2.6e-01 5.7e-15 1.2e-01 9.60e-01 3.596246600e+01 3.398708338e+01 3.8e-02 0.01
3 3.5e-02 3.4e-14 1.4e-02 1.17e+00 3.590440920e+01 3.566690230e+01 5.0e-03 0.01
4 3.8e-03 2.2e-14 5.6e-04 1.03e+00 3.594107223e+01 3.591508466e+01 5.6e-04 0.01
5 4.4e-04 5.1e-14 2.2e-05 1.01e+00 3.594136121e+01 3.593843210e+01 6.3e-05 0.01
6 6.9e-05 2.1e-13 1.5e-06 1.00e+00 3.594075920e+01 3.594029396e+01 1.0e-05 0.02
7 9.8e-06 5.6e-13 7.9e-08 1.00e+00 3.594077965e+01 3.594071398e+01 1.4e-06 0.02
8 1.9e-08 3.0e-12 6.8e-12 1.00e+00 3.594077695e+01 3.594077682e+01 2.8e-09 0.02
Optimizer terminated. Time: 0.02
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 3.5940776947e+01 nrm: 2e+01 Viol. con: 6e-08 var: 7e-09 cones: 0e+00
Dual. obj: 3.5940776819e+01 nrm: 1e+00 Viol. con: 0e+00 var: 6e-10 cones: 0e+00
Optimizer summary
Optimizer - time: 0.02
Interior-point - iterations : 8 time: 0.02
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +35.9408
Found a feasible x in R^50 that has 44 nonzeros using the l1-norm heuristic.
Log-based heuristic:
found a solution with 44 nonzeros...
found a solution with 37 nonzeros...
found a solution with 35 nonzeros...
found a solution with 35 nonzeros...
found a solution with 35 nonzeros...
found a solution with 35 nonzeros...
found a solution with 35 nonzeros...
found a solution with 35 nonzeros...
found a solution with 35 nonzeros...
found a solution with 35 nonzeros...
found a solution with 35 nonzeros...
found a solution with 35 nonzeros...
found a solution with 35 nonzeros...
found a solution with 35 nonzeros...
found a solution with 35 nonzeros...
Found a feasible x in R^50 that has 35 nonzeros using the log heuristic.