% S. Boyd, et. al., "Convex Optimization of Graph Laplacian Eigenvalues"
% ICM'06 talk examples (www.stanford.edu/~boyd/cvx_opt_graph_lapl_eigs.html)
% Written for CVX by Almir Mutapcic 08/29/06
% (figures are generated)
%
% In this example we consider a graph described by the incidence matrix A.
% Each edge has a weight W_i, and we optimize various functions of the
% edge weights as described in the referenced paper; in particular,
%
% - the fastest distributed linear averaging (FDLA) problem (fdla.m)
% - the fastest mixing Markov chain (FMMC) problem (fmmc.m)
%
% Then we compare these solutions to the heuristics listed below:
%
% - maximum-degree heuristic (max_deg.m)
% - constant weights that yield fastest averaging (best_const.m)
% - Metropolis-Hastings heuristic (mh.m)

% generate a cut-grid graph example
[A,xy] = cut_grid_data;

% Compute edge weights: some optimal, some based on heuristics
[n,m] = size(A);

[ w_fdla, rho_fdla ] = fdla(A);
[ w_fmmc, rho_fmmc ] = fmmc(A);
[ w_md,   rho_md   ] = max_deg(A);
[ w_bc,   rho_bc   ] = best_const(A);
[ w_mh,   rho_mh   ] = mh(A);

tau_fdla = 1/log(1/rho_fdla);
tau_fmmc = 1/log(1/rho_fmmc);
tau_md   = 1/log(1/rho_md);
tau_bc   = 1/log(1/rho_bc);
tau_mh   = 1/log(1/rho_mh);

fprintf(1,'\nResults:\n');
fprintf(1,'FDLA weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_fdla,tau_fdla);
fprintf(1,'FMMC weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_fmmc,tau_fmmc);
fprintf(1,'M-H weights:\t\t rho = %5.4f \t tau = %5.4f\n',rho_mh,tau_mh);
fprintf(1,'MAX_DEG weights:\t rho = %5.4f \t tau = %5.4f\n',rho_md,tau_md);
fprintf(1,'BEST_CONST weights:\t rho = %5.4f \t tau = %5.4f\n',rho_bc,tau_bc);

% plot results
figure(1), clf
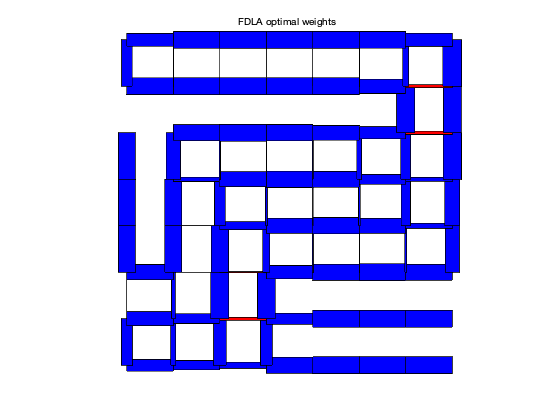
plotgraph(A,xy,w_fdla);
text(0.425,1.05,'FDLA optimal weights')

figure(2), clf
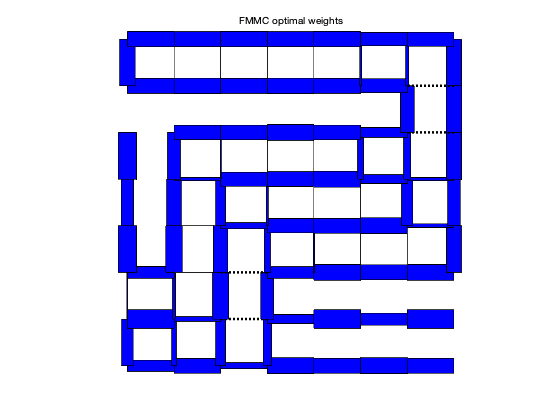
plotgraph(A,xy,w_fmmc);
text(0.425,1.05,'FMMC optimal weights')

figure(3), clf
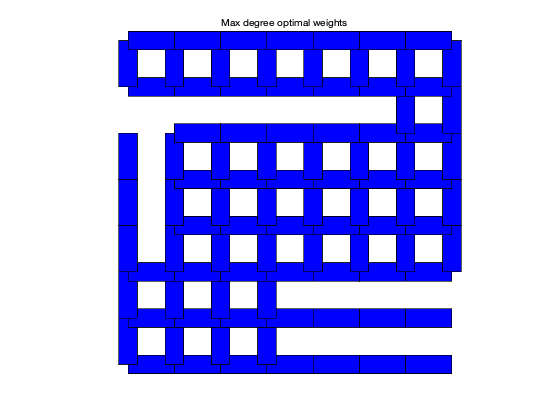
plotgraph(A,xy,w_md);
text(0.375,1.05,'Max degree optimal weights')

figure(4), clf
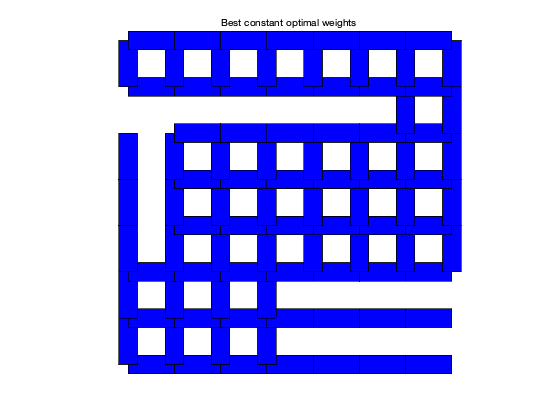
plotgraph(A,xy,w_bc);
text(0.375,1.05,'Best constant optimal weights')

figure(5), clf
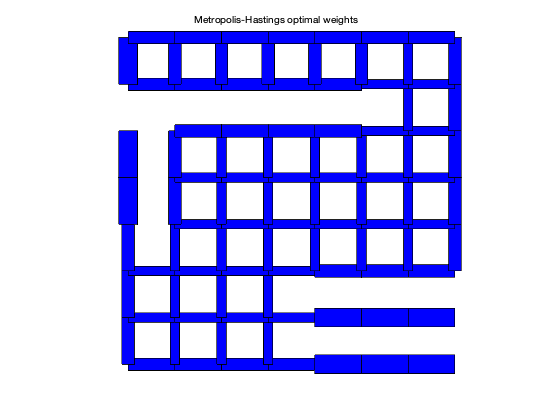
plotgraph(A,xy,w_mh);
text(0.3,1.05,'Metropolis-Hastings optimal weights')

 
Calling Mosek 9.1.9: 4184 variables, 120 equality constraints
   For improved efficiency, Mosek is solving the dual problem.
------------------------------------------------------------

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86

Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 120             
  Cones                  : 0               
  Scalar variables       : 24              
  Matrix variables       : 2               
  Integer variables      : 0               

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries                  : 2                 time                   : 0.00            
Lin. dep.  - tries                  : 1                 time                   : 0.00            
Lin. dep.  - number                 : 0               
Presolve terminated. Time: 0.00    
Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 120             
  Cones                  : 0               
  Scalar variables       : 24              
  Matrix variables       : 2               
  Integer variables      : 0               

Optimizer  - threads                : 8               
Optimizer  - solved problem         : the primal      
Optimizer  - Constraints            : 120
Optimizer  - Cones                  : 1
Optimizer  - Scalar variables       : 25                conic                  : 25              
Optimizer  - Semi-definite variables: 2                 scalarized             : 4160            
Factor     - setup time             : 0.00              dense det. time        : 0.00            
Factor     - ML order time          : 0.00              GP order time          : 0.00            
Factor     - nonzeros before factor : 7260              after factor           : 7260            
Factor     - dense dim.             : 0                 flops                  : 2.43e+06        
ITE PFEAS    DFEAS    GFEAS    PRSTATUS   POBJ              DOBJ              MU       TIME  
0   3.2e+01  2.0e+00  1.0e+00  0.00e+00   0.000000000e+00   0.000000000e+00   1.0e+00  0.01  
1   3.1e+00  1.9e-01  2.0e-01  -8.72e-01  -8.019510317e+00  -4.401131508e+00  9.8e-02  0.02  
2   1.2e+00  7.7e-02  1.3e-02  1.89e+00   -2.718140559e+00  -2.709331389e+00  3.9e-02  0.02  
3   4.3e-01  2.7e-02  3.2e-03  3.77e+00   -1.042480075e+00  -1.000747146e+00  1.3e-02  0.02  
4   1.0e-01  6.4e-03  3.5e-04  1.16e+00   -1.020758837e+00  -1.012170926e+00  3.2e-03  0.03  
5   2.2e-02  1.4e-03  3.5e-05  1.07e+00   -9.933590824e-01  -9.916179623e-01  7.1e-04  0.03  
6   4.3e-03  2.7e-04  2.8e-06  1.01e+00   -9.900646661e-01  -9.897875730e-01  1.4e-04  0.04  
7   1.6e-03  1.0e-04  6.0e-07  1.00e+00   -9.886708058e-01  -9.885799220e-01  5.1e-05  0.04  
8   5.5e-04  3.4e-05  1.1e-07  1.00e+00   -9.884275770e-01  -9.884069306e-01  1.7e-05  0.04  
9   1.4e-04  8.7e-06  1.3e-08  1.00e+00   -9.883031046e-01  -9.882987307e-01  4.4e-06  0.05  
10  2.2e-05  1.4e-06  7.1e-10  1.00e+00   -9.882948441e-01  -9.882944267e-01  6.8e-07  0.05  
11  2.7e-06  1.7e-07  3.2e-11  1.00e+00   -9.882922134e-01  -9.882921630e-01  8.6e-08  0.05  
12  2.0e-07  1.2e-08  6.0e-13  1.00e+00   -9.882919077e-01  -9.882919043e-01  6.2e-09  0.06  
13  1.3e-08  9.3e-10  1.0e-14  1.00e+00   -9.882918850e-01  -9.882918847e-01  4.1e-10  0.06  
Optimizer terminated. Time: 0.07    


Interior-point solution summary
  Problem status  : PRIMAL_AND_DUAL_FEASIBLE
  Solution status : OPTIMAL
  Primal.  obj: -9.8829188496e-01   nrm: 1e+00    Viol.  con: 5e-08    var: 0e+00    barvar: 0e+00  
  Dual.    obj: -9.8829188474e-01   nrm: 1e+00    Viol.  con: 0e+00    var: 4e-10    barvar: 9e-10  
Optimizer summary
  Optimizer                 -                        time: 0.07    
    Interior-point          - iterations : 13        time: 0.06    
      Basis identification  -                        time: 0.00    
        Primal              - iterations : 0         time: 0.00    
        Dual                - iterations : 0         time: 0.00    
        Clean primal        - iterations : 0         time: 0.00    
        Clean dual          - iterations : 0         time: 0.00    
    Simplex                 -                        time: 0.00    
      Primal simplex        - iterations : 0         time: 0.00    
      Dual simplex          - iterations : 0         time: 0.00    
    Mixed integer           - relaxations: 0         time: 0.00    

------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.988292
 
 
Calling Mosek 9.1.9: 4366 variables, 143 equality constraints
   For improved efficiency, Mosek is solving the dual problem.
------------------------------------------------------------

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86

Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 143             
  Cones                  : 0               
  Scalar variables       : 206             
  Matrix variables       : 2               
  Integer variables      : 0               

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries                  : 2                 time                   : 0.00            
Lin. dep.  - tries                  : 1                 time                   : 0.00            
Lin. dep.  - number                 : 0               
Presolve terminated. Time: 0.00    
Problem
  Name                   :                 
  Objective sense        : min             
  Type                   : CONIC (conic optimization problem)
  Constraints            : 143             
  Cones                  : 0               
  Scalar variables       : 206             
  Matrix variables       : 2               
  Integer variables      : 0               

Optimizer  - threads                : 8               
Optimizer  - solved problem         : the primal      
Optimizer  - Constraints            : 143
Optimizer  - Cones                  : 1
Optimizer  - Scalar variables       : 207               conic                  : 48              
Optimizer  - Semi-definite variables: 2                 scalarized             : 4160            
Factor     - setup time             : 0.00              dense det. time        : 0.00            
Factor     - ML order time          : 0.00              GP order time          : 0.00            
Factor     - nonzeros before factor : 1.03e+04          after factor           : 1.03e+04        
Factor     - dense dim.             : 0                 flops                  : 2.83e+06        
ITE PFEAS    DFEAS    GFEAS    PRSTATUS   POBJ              DOBJ              MU       TIME  
0   1.3e+02  2.0e+00  1.0e+00  0.00e+00   0.000000000e+00   0.000000000e+00   1.0e+00  0.01  
1   5.1e+01  7.9e-01  7.9e-02  8.11e-01   -3.046146012e-01  -5.763859839e-01  4.0e-01  0.02  
2   1.0e+01  1.6e-01  6.5e-03  1.22e+00   -8.862518414e-01  -9.308217049e-01  7.9e-02  0.02  
3   3.7e-01  5.7e-03  9.2e-05  1.15e+00   -9.979998593e-01  -9.987091101e-01  2.9e-03  0.03  
4   9.1e-02  1.4e-03  1.1e-05  1.03e+00   -9.935245223e-01  -9.936931348e-01  7.1e-04  0.03  
5   2.1e-02  3.2e-04  1.2e-06  1.02e+00   -9.912583259e-01  -9.912972989e-01  1.6e-04  0.03  
6   9.1e-03  1.4e-04  3.5e-07  1.03e+00   -9.899472992e-01  -9.899645638e-01  7.1e-05  0.04  
7   4.6e-03  7.1e-05  1.3e-07  1.03e+00   -9.893460524e-01  -9.893547576e-01  3.6e-05  0.04  
8   2.6e-03  4.1e-05  5.5e-08  1.02e+00   -9.891541777e-01  -9.891591871e-01  2.1e-05  0.04  
9   9.2e-04  1.4e-05  1.1e-08  1.01e+00   -9.889286588e-01  -9.889304051e-01  7.2e-06  0.05  
10  4.2e-04  6.5e-06  3.4e-09  1.01e+00   -9.888803217e-01  -9.888811176e-01  3.3e-06  0.05  
11  1.5e-04  2.3e-06  7.1e-10  1.01e+00   -9.888444131e-01  -9.888446958e-01  1.2e-06  0.06  
12  6.7e-05  1.0e-06  2.2e-10  1.00e+00   -9.888354479e-01  -9.888355757e-01  5.3e-07  0.06  
13  1.4e-05  2.2e-07  2.1e-11  1.00e+00   -9.888280617e-01  -9.888280892e-01  1.1e-07  0.07  
14  4.1e-06  6.4e-08  3.3e-12  1.00e+00   -9.888267289e-01  -9.888267368e-01  3.2e-08  0.07  
15  1.2e-06  1.9e-08  5.5e-13  1.00e+00   -9.888263244e-01  -9.888263268e-01  9.8e-09  0.07  
16  4.7e-07  7.3e-09  1.3e-13  9.99e-01   -9.888262223e-01  -9.888262232e-01  3.7e-09  0.08  
17  1.4e-07  2.4e-09  2.0e-14  1.00e+00   -9.888261734e-01  -9.888261737e-01  1.1e-09  0.08  
18  4.6e-08  1.2e-08  3.8e-15  1.00e+00   -9.888261614e-01  -9.888261615e-01  3.6e-10  0.08  
Optimizer terminated. Time: 0.09    


Interior-point solution summary
  Problem status  : PRIMAL_AND_DUAL_FEASIBLE
  Solution status : OPTIMAL
  Primal.  obj: -9.8882616142e-01   nrm: 1e+00    Viol.  con: 3e-08    var: 2e-11    barvar: 0e+00  
  Dual.    obj: -9.8882616151e-01   nrm: 1e+00    Viol.  con: 0e+00    var: 2e-10    barvar: 7e-09  
Optimizer summary
  Optimizer                 -                        time: 0.09    
    Interior-point          - iterations : 18        time: 0.09    
      Basis identification  -                        time: 0.00    
        Primal              - iterations : 0         time: 0.00    
        Dual                - iterations : 0         time: 0.00    
        Clean primal        - iterations : 0         time: 0.00    
        Clean dual          - iterations : 0         time: 0.00    
    Simplex                 -                        time: 0.00    
      Primal simplex        - iterations : 0         time: 0.00    
      Dual simplex          - iterations : 0         time: 0.00    
    Mixed integer           - relaxations: 0         time: 0.00    

------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.988826
 

Results:
FDLA weights:		 rho = 0.9883 	 tau = 84.9099
FMMC weights:		 rho = 0.9888 	 tau = 88.9938
M-H weights:		 rho = 0.9917 	 tau = 120.2442
MAX_DEG weights:	 rho = 0.9927 	 tau = 136.7523
BEST_CONST weights:	 rho = 0.9921 	 tau = 126.3450