clear
rand('state',29);
noiseint=.05;
u = [0:0.04:2]';
m=length(u);
y = 5*(u-1).^4 + .6*(u-1).^2 + 0.5*u;
v1=u>=.2;
v2=u<=.6;
v3=v1.*v2;
dipvec=((v3.*u-.4*ones(1,size(v3,2))).^(2)).*v3;
y=y+40*(dipvec-((.2))^2*v3);
randf=noiseint*(rand(m,1)-.5);
yns=y+norm(y)*(randf);
figure
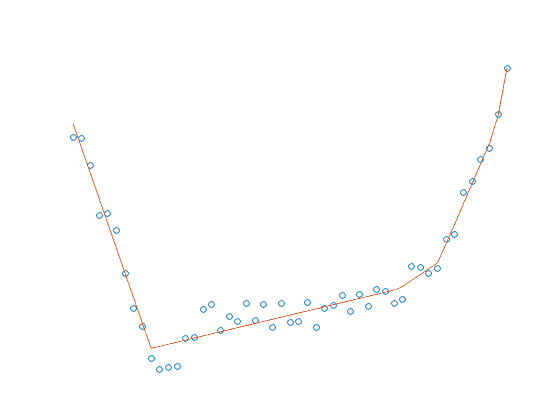
plot(u,yns,'o');
cvx_begin
variables yhat(m) g(m)
minimize(norm(yns-yhat))
subject to
yhat*ones(1,m) >= ones(m,1)*yhat' + (ones(m,1)*g').*(u*ones(1,m)-ones(m,1)*u');
cvx_end
nopts =1000;
t = linspace(0,2,nopts);
f = max(yhat(:,ones(1,nopts)) + ...
g(:,ones(1,nopts)).*(t(ones(m,1),:)-u(:,ones(1,nopts))));
plot(u,yns,'o',t,f,'-');
axis off
Calling Mosek 9.1.9: 2602 variables, 103 equality constraints
For improved efficiency, Mosek is solving the dual problem.
------------------------------------------------------------
MOSEK Version 9.1.9 (Build date: 2019-11-21 11:32:15)
Copyright (c) MOSEK ApS, Denmark. WWW: mosek.com
Platform: MACOSX/64-X86
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 103
Cones : 1
Scalar variables : 2602
Matrix variables : 0
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 1 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.00
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 103
Cones : 1
Scalar variables : 2602
Matrix variables : 0
Integer variables : 0
Optimizer - threads : 8
Optimizer - solved problem : the primal
Optimizer - Constraints : 100
Optimizer - Cones : 1
Optimizer - Scalar variables : 2502 conic : 52
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 3874 after factor : 5050
Factor - dense dim. : 0 flops : 3.71e+05
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 1.0e+00 7.9e+00 2.0e+00 0.00e+00 0.000000000e+00 -1.000000000e+00 1.0e+00 0.00
1 4.0e-01 3.2e+00 1.0e+00 -8.04e-01 -2.411440521e+00 -2.370632537e+00 4.0e-01 0.01
2 9.9e-02 7.8e-01 2.2e-01 -2.37e-01 -4.901628796e+00 -4.291091481e+00 9.9e-02 0.01
3 2.1e-02 1.6e-01 2.2e-02 6.31e-01 -5.225708045e+00 -5.095297522e+00 2.1e-02 0.01
4 3.6e-03 2.9e-02 1.5e-03 1.01e+00 -5.317798571e+00 -5.301114814e+00 3.6e-03 0.02
5 5.2e-04 4.1e-03 8.0e-05 1.04e+00 -5.192975323e+00 -5.190743539e+00 5.2e-04 0.02
6 3.9e-04 3.1e-03 5.4e-05 9.00e-01 -4.828858712e+00 -4.826977695e+00 3.9e-04 0.02
7 3.5e-04 2.7e-03 4.6e-05 7.61e-01 -4.632061026e+00 -4.630190100e+00 3.5e-04 0.02
8 3.0e-04 2.4e-03 3.8e-05 8.93e-01 -4.463375636e+00 -4.461799341e+00 3.0e-04 0.02
9 2.4e-04 1.9e-03 2.8e-05 7.14e-01 -4.075779742e+00 -4.074227721e+00 2.4e-04 0.02
10 1.7e-04 1.4e-03 1.7e-05 9.03e-01 -3.762806997e+00 -3.761754840e+00 1.7e-04 0.02
11 1.1e-04 8.9e-04 9.6e-06 7.52e-01 -3.228831403e+00 -3.227990075e+00 1.1e-04 0.02
12 6.5e-05 5.2e-04 4.2e-06 9.55e-01 -2.974940962e+00 -2.974487008e+00 6.5e-05 0.02
13 3.2e-05 2.5e-04 1.5e-06 8.68e-01 -2.579655374e+00 -2.579395159e+00 3.2e-05 0.02
14 1.4e-05 1.1e-04 4.6e-07 9.99e-01 -2.471441621e+00 -2.471322262e+00 1.4e-05 0.02
15 3.8e-06 3.0e-05 6.3e-08 9.75e-01 -2.322286314e+00 -2.322251513e+00 3.8e-06 0.03
16 1.2e-06 9.2e-06 1.1e-08 1.00e+00 -2.291714195e+00 -2.291703000e+00 1.2e-06 0.03
17 1.3e-07 1.0e-06 3.9e-10 9.99e-01 -2.276071639e+00 -2.276070399e+00 1.3e-07 0.03
18 1.3e-08 1.0e-07 1.2e-11 1.00e+00 -2.274446781e+00 -2.274446656e+00 1.3e-08 0.03
19 3.8e-10 3.0e-09 6.4e-14 1.00e+00 -2.274271282e+00 -2.274271278e+00 3.8e-10 0.03
Optimizer terminated. Time: 0.03
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: -2.2742712819e+00 nrm: 1e+00 Viol. con: 3e-13 var: 1e-09 cones: 0e+00
Dual. obj: -2.2742712781e+00 nrm: 6e+01 Viol. con: 0e+00 var: 1e-08 cones: 0e+00
Optimizer summary
Optimizer - time: 0.03
Interior-point - iterations : 19 time: 0.03
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +2.27427